Cara Menghitung Kuartil Data Dan Interpretasinya, nggak seseram yang dibayangkan, kok! Mempelajari kuartil itu seperti membuka rahasia tersembunyi di balik data-data angka. Bayangkan kamu punya sekumpulan nilai ujian, dengan kuartil, kamu bisa tahu seberapa menyebar nilai tersebut, siapa yang berada di kelompok atas, tengah, dan bawah. Lebih dari itu, kamu bisa mengidentifikasi nilai-nilai ekstrem atau outlier yang mungkin perlu diteliti lebih lanjut.
Siap menguasai ilmu statistik yang satu ini dan menaklukkan dunia data?
Kuartil membagi data menjadi empat bagian yang sama besar, memberikan gambaran yang lebih komprehensif dibandingkan hanya melihat rata-rata. Kita akan belajar cara menghitung kuartil untuk data tunggal dan data berkelompok, serta bagaimana menginterpretasikan hasilnya untuk pengambilan keputusan yang lebih cerdas. Dengan memahami kuartil, kamu bisa menganalisis data dengan lebih akurat dan efektif, baik untuk keperluan akademik, pekerjaan, maupun kehidupan sehari-hari.
Yuk, kita mulai!
Memahami Kuartil: Panduan Lengkap untuk Analisis Data: Cara Menghitung Kuartil Data Dan Interpretasinya
Hai, Fimelova! Ngomongin data, nggak cuma rata-rata aja yang penting, lho! Ada hal lain yang bisa kasih kamu insight lebih dalam, yaitu kuartil. Kuartil adalah alat statistik yang super berguna untuk memahami sebaran data dan mengidentifikasi pola-pola tersembunyi. Yuk, kita bahas tuntas!
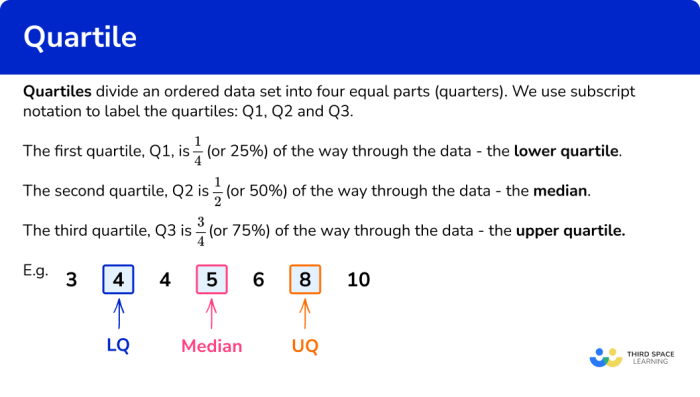
Pengertian Kuartil
Kuartil dalam statistika adalah nilai yang membagi data terurut menjadi empat bagian yang sama besar. Bayangkan kamu punya sekumpulan data, kuartil akan membagi data tersebut menjadi 25% bagian pertama, 25% bagian kedua, 25% bagian ketiga, dan 25% bagian terakhir.
Contoh sederhana: Misalnya, nilai ujian 5 siswa adalah: 60, 70, 80, 90, 100. Setelah diurutkan, Q1 (kuartil pertama) adalah 70, Q2 (kuartil kedua atau median) adalah 80, dan Q3 (kuartil ketiga) adalah 90.
| Kuartil | Nilai | Persentase Data | Interpretasi |
|---|---|---|---|
| Q1 (Kuartil Pertama) | Memisahkan 25% data terendah dari 75% data tertinggi | 25% | Menunjukkan batas bawah dari 25% data terbesar |
| Q2 (Kuartil Kedua/Median) | Memisahkan 50% data terendah dari 50% data tertinggi | 50% | Menunjukkan nilai tengah dari seluruh data |
| Q3 (Kuartil Ketiga) | Memisahkan 75% data terendah dari 25% data tertinggi | 75% | Menunjukkan batas atas dari 25% data terkecil |
Kegunaan kuartil sangat luas, mulai dari memahami distribusi pendapatan, menganalisis nilai ujian, hingga mengidentifikasi outlier (nilai ekstrem) dalam data. Dengan memahami kuartil, kamu bisa mendapatkan gambaran yang lebih komprehensif tentang data yang sedang dianalisa.
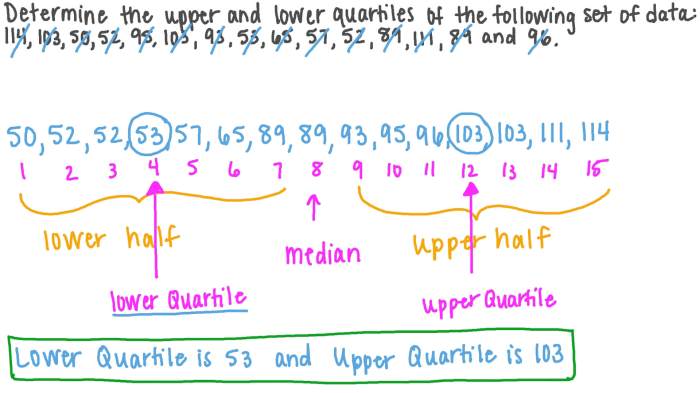
Cara Menghitung Kuartil Data
Cara menghitung kuartil berbeda tergantung jenis data: data tunggal (diskrit) atau data berkelompok (kontinu).
Menghitung Kuartil untuk Data Tunggal
Langkah-langkah menghitung kuartil untuk data tunggal cukup sederhana. Pertama, urutkan data dari terkecil ke terbesar. Kemudian, tentukan posisi Q1, Q2, dan Q3 menggunakan rumus berikut:
- Posisi Q1 = (n+1)/4
- Posisi Q2 = (n+1)/2
- Posisi Q3 = 3(n+1)/4
di mana ‘n’ adalah jumlah data. Jika hasilnya bukan bilangan bulat, gunakan interpolasi linier untuk mendapatkan nilai kuartil.
Contoh: Data: 2, 4, 6, 8, 10. n = 5. Posisi Q1 = (5+1)/4 = 1.5. Artinya Q1 berada di antara data ke-1 dan ke-2, yaitu (2+4)/2 = 3. Posisi Q2 = (5+1)/2 = 3, sehingga Q2 = 6.
Posisi Q3 = 3(5+1)/4 = 4.5, sehingga Q3 = (8+10)/2 = 9.
Menghitung Kuartil untuk Data Berkelompok
Untuk data berkelompok, perhitungan kuartil sedikit lebih kompleks. Kita membutuhkan tabel frekuensi dan rumus berikut:
Qi = L i + [((n/4)i – F k)/f i]c
di mana:
- Q i = kuartil ke-i (i = 1, 2, 3)
- L i = batas bawah kelas interval yang memuat kuartil ke-i
- n = jumlah data
- F k = frekuensi kumulatif sebelum kelas interval yang memuat kuartil ke-i
- f i = frekuensi kelas interval yang memuat kuartil ke-i
- c = panjang kelas interval
Contoh perhitungan untuk data berkelompok akan membutuhkan tabel frekuensi yang spesifik. Misalnya, data tinggi badan siswa. Setelah tabel frekuensi dibuat, kita bisa menghitung Q1, Q2, dan Q3 menggunakan rumus di atas dengan mengganti nilai-nilai yang sesuai.
Langkah-langkah perhitungan kuartil untuk data berkelompok adalah:
- Buat tabel frekuensi data.
- Hitung frekuensi kumulatif.
- Tentukan posisi kuartil (n/4 untuk Q1, n/2 untuk Q2, 3n/4 untuk Q3).
- Identifikasi kelas interval yang memuat kuartil.
- Hitung nilai kuartil menggunakan rumus yang telah disebutkan di atas.
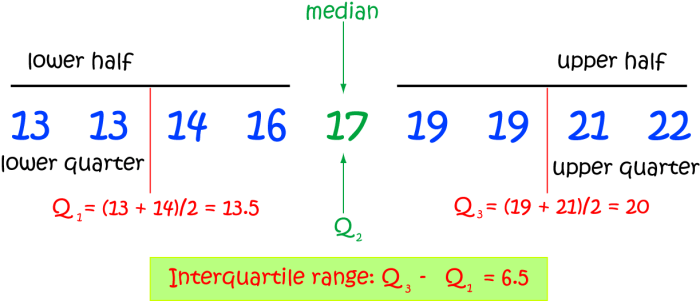
Interpretasi Kuartil, Cara Menghitung Kuartil Data Dan Interpretasinya

Setiap kuartil memiliki arti tersendiri dalam konteks distribusi data.
- Q1: Menunjukkan 25% data terendah. Misalnya, dalam data pendapatan, Q1 menunjukkan batas bawah 25% pendapatan terendah.
- Q2 (Median): Menunjukkan nilai tengah data. 50% data berada di bawah median dan 50% di atasnya.
- Q3: Menunjukkan 75% data terendah. Dalam contoh pendapatan, Q3 menunjukkan batas atas 25% pendapatan terendah.
Rentang antar kuartil (IQR = Q3 – Q1) menunjukkan sebaran data. IQR yang besar mengindikasikan sebaran data yang luas, sedangkan IQR yang kecil menunjukkan sebaran data yang sempit. IQR juga berguna untuk mendeteksi outlier. Data yang berada di luar batas (Q1 – 1.5*IQR) dan (Q3 + 1.5*IQR) dapat dianggap sebagai outlier.
Interpretasi kuartil sangat membantu dalam pengambilan keputusan. Misalnya, dalam bisnis, memahami sebaran pendapatan pelanggan dapat membantu dalam menentukan strategi pemasaran yang tepat.
Penerapan Kuartil dalam Berbagai Konteks

Kuartil memiliki aplikasi yang luas dalam berbagai bidang.
Analisis pendapatan rumah tangga: Kuartil dapat digunakan untuk membagi penduduk menjadi kelompok-kelompok berdasarkan pendapatan mereka (misalnya, 25% terkaya, 25% termiskin, dll.).
Analisis nilai ujian siswa: Kuartil membantu memahami sebaran nilai ujian, mengidentifikasi siswa yang berkinerja baik dan yang membutuhkan bantuan tambahan. Misalnya, Q1 bisa menunjukkan batas nilai siswa yang perlu remedial.
Menentukan posisi suatu nilai dalam distribusi data: Kuartil memberikan gambaran tentang posisi relatif suatu nilai dalam distribusi data. Misalnya, jika nilai seseorang berada di atas Q3, maka nilainya termasuk dalam 25% nilai tertinggi.
Visualisasi data dengan box plot: Box plot adalah grafik yang menampilkan kuartil, median, dan outlier. Box plot menunjukkan sebaran data dengan jelas dan mudah dipahami. Box menunjukkan rentang interkuartil (IQR), garis di dalam box menunjukkan median, dan titik-titik di luar box menunjukkan outlier.
Keuntungan menggunakan kuartil dibandingkan rata-rata adalah kuartil tidak dipengaruhi oleh outlier. Rata-rata dapat terpengaruh secara signifikan oleh nilai ekstrem, sedangkan kuartil tetap memberikan gambaran yang akurat tentang sebaran data meskipun ada outlier.
Penutup
Memahami cara menghitung kuartil data dan interpretasinya membuka pintu menuju analisis data yang lebih mendalam. Dengan kemampuan ini, kamu tidak hanya bisa melihat gambaran umum data, tetapi juga mengidentifikasi tren, pola, dan outlier yang mungkin tersembunyi. Kemampuan menganalisis data dengan kuartil akan sangat berharga, baik untuk menganalisis data penjualan, nilai ujian, pendapatan rumah tangga, maupun data lainnya.
Jadi, jangan ragu untuk mempraktikkan ilmu baru ini dan manfaatkan kekuatan kuartil untuk pengambilan keputusan yang lebih baik!
Informasi FAQ
Apa perbedaan antara kuartil dan desil?
Kuartil membagi data menjadi empat bagian sama besar, sedangkan desil membagi data menjadi sepuluh bagian sama besar.
Bagaimana jika ada data yang sama persis pada titik kuartil?
Jika terdapat data kembar pada titik kuartil, nilai kuartil tersebut adalah nilai data kembar tersebut.
Apakah kuartil selalu tepat di tengah-tengah data?
Tidak, posisi kuartil bergantung pada jumlah data dan cara perhitungannya, tidak selalu tepat di tengah.
Bisakah kuartil digunakan untuk data kualitatif?
Tidak, kuartil hanya dapat digunakan untuk data kuantitatif (numerik).