Kurva Lorenz: Pengertian Dan Interpretasinya, siapa sangka sebuah kurva bisa begitu powerful dalam menggambarkan kesenjangan? Bayangkan, sebuah garis lengkung sederhana mampu mengungkap sebaran kekayaan atau pendapatan suatu negara, bahkan hingga distribusi akses kesehatan! Dengan memahami Kurva Lorenz, kita bisa melihat gambaran nyata tentang keadilan ekonomi dan sosial. Siap-siap tercengang dengan kekuatan visualisasi data yang satu ini!
Kurva Lorenz merupakan alat visual yang efektif untuk menggambarkan tingkat ketimpangan distribusi suatu variabel, seperti pendapatan, kekayaan, atau bahkan akses terhadap layanan kesehatan. Ia membandingkan distribusi kumulatif ideal (distribusi sempurna merata) dengan distribusi kumulatif aktual. Semakin jauh kurva Lorenz dari garis diagonal sempurna (garis kemerataan), semakin besar tingkat ketimpangannya. Konsep ini dipadukan dengan Koefisien Gini, yang memberikan angka kuantitatif untuk mengukur tingkat ketimpangan tersebut.
Pemahaman Kurva Lorenz dan Koefisien Gini sangat penting dalam menganalisis kesenjangan sosial dan ekonomi, dan membantu dalam merumuskan kebijakan publik yang lebih adil dan inklusif.
Kurva Lorenz: Memahami Distribusi Kekayaan dan Pendapatan
Pernahkah kamu bertanya-tanya seberapa merata kekayaan atau pendapatan di suatu negara? Kurva Lorenz hadir sebagai alat visual yang ampuh untuk menjawab pertanyaan tersebut. Dengan bentuknya yang unik, kurva ini mampu menggambarkan tingkat ketimpangan distribusi, memberikan gambaran yang lebih jelas daripada sekadar angka statistik rata-rata. Yuk, kita telusuri lebih dalam tentang Kurva Lorenz, dari pengertian hingga penerapannya dalam berbagai bidang!
Pengertian Kurva Lorenz
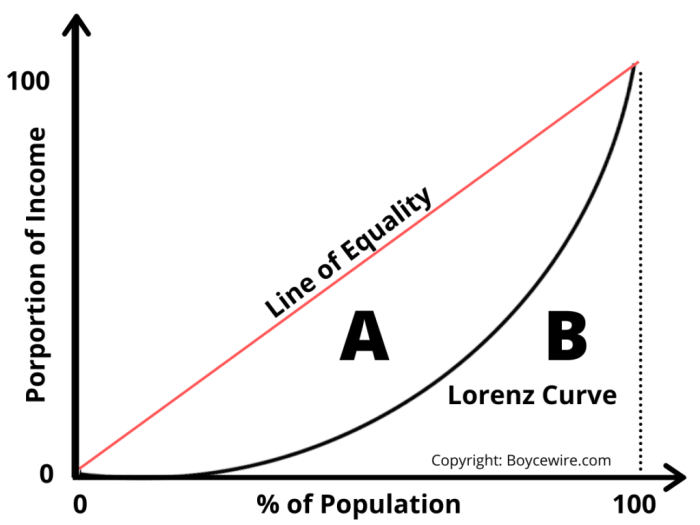
Kurva Lorenz adalah representasi grafis yang menunjukkan distribusi suatu variabel, misalnya pendapatan atau kekayaan, di antara populasi. Sumbu X menunjukkan persentase kumulatif populasi (misalnya, 20% penduduk termiskin), sedangkan sumbu Y menunjukkan persentase kumulatif variabel yang didistribusikan (misalnya, 10% total pendapatan). Kurva ini membandingkan distribusi aktual dengan distribusi sempurna yang merata (garis diagonal 45 derajat). Semakin jauh kurva dari garis diagonal, semakin besar ketimpangan distribusi tersebut.
Contoh penerapannya dalam ekonomi adalah menggambarkan distribusi pendapatan di suatu negara. Misalnya, jika kurva Lorenz untuk pendapatan di Indonesia menjauhi garis diagonal, hal ini mengindikasikan adanya ketimpangan pendapatan yang signifikan. Sebaliknya, kurva yang mendekati garis diagonal menandakan distribusi pendapatan yang lebih merata.
Kurva Lorenz menggambarkan distribusi pendapatan atau kekayaan dengan menunjukkan proporsi kumulatif populasi yang memiliki proporsi kumulatif tertentu dari total pendapatan atau kekayaan. Dengan demikian, kita dapat melihat dengan jelas apakah distribusi tersebut merata atau tidak.
Berbeda dengan kurva distribusi lainnya seperti kurva Pareto yang fokus pada distribusi frekuensi, Kurva Lorenz lebih menekankan pada distribusi kumulatif. Kurva Pareto sering digunakan untuk menggambarkan distribusi 80/20, di mana 20% dari populasi memiliki 80% dari sumber daya. Sementara itu, Kurva Lorenz memberikan gambaran yang lebih komprehensif tentang distribusi di seluruh rentang populasi.
| Nama Kurva | Karakteristik Utama | Kegunaan | Keterbatasan |
|---|---|---|---|
| Kurva Lorenz | Menunjukkan distribusi kumulatif suatu variabel; Membandingkan distribusi aktual dengan distribusi ideal; Digambarkan secara grafis. | Menganalisis ketimpangan distribusi pendapatan, kekayaan, atau sumber daya lainnya; Membandingkan distribusi antar kelompok atau negara. | Tidak menunjukkan besarnya ketimpangan secara kuantitatif; Membutuhkan data yang akurat dan terpercaya; Bisa menyesatkan jika tidak diinterpretasi dengan hati-hati. |
| Kurva Pareto | Menunjukkan distribusi frekuensi yang mengikuti prinsip 80/20; Sering digunakan untuk menganalisis distribusi sumber daya yang tidak merata. | Menganalisis efisiensi, mengidentifikasi faktor-faktor penting yang berkontribusi pada hasil, menentukan prioritas. | Sederhana, hanya menunjukkan distribusi secara umum; Tidak memberikan gambaran detail tentang distribusi di seluruh rentang. |
Konsep Koefisien Gini
Koefisien Gini merupakan ukuran kuantitatif yang menggambarkan ketimpangan distribusi, yang diturunkan dari Kurva Lorenz. Nilai Koefisien Gini berkisar antara 0 hingga 1. Nilai 0 menunjukkan distribusi yang sempurna merata, sedangkan nilai 1 menunjukkan ketimpangan yang sempurna (satu orang memiliki semua sumber daya).
Koefisien Gini dihitung dengan menghitung luas area di antara Kurva Lorenz dan garis diagonal sempurna, kemudian membaginya dengan luas segitiga di bawah garis diagonal. Rumus yang lebih tepat dan kompleks melibatkan integral, namun prinsip dasarnya tetap sama.
Contoh perhitungan: Misalkan kita memiliki data distribusi pendapatan hipotetis dengan 5 kelompok penduduk: (10%, 5%), (20%, 15%), (30%, 25%), (40%, 40%), (50%, 60%). Dengan menggunakan metode numerik (trapezoidal rule atau lainnya), kita bisa memperkirakan luas area di antara Kurva Lorenz dan garis diagonal, lalu menghitung Koefisien Gini. Nilai yang dihasilkan akan menunjukkan tingkat ketimpangan pendapatan.
Nilai Koefisien Gini yang mendekati 0 menunjukkan distribusi yang relatif merata, sementara nilai mendekati 1 menunjukkan distribusi yang sangat tidak merata. Sebagai contoh, negara dengan sistem kesejahteraan sosial yang kuat cenderung memiliki Koefisien Gini yang lebih rendah dibandingkan negara dengan kesenjangan ekonomi yang besar.
Diagram perubahan distribusi pendapatan dan pengaruhnya terhadap Kurva Lorenz dan Koefisien Gini akan menunjukkan dua Kurva Lorenz: satu dengan Koefisien Gini rendah (dekat dengan garis diagonal, menunjukkan distribusi merata), dan satu lagi dengan Koefisien Gini tinggi (jauh dari garis diagonal, menunjukkan distribusi tidak merata). Perubahan distribusi pendapatan akan digambarkan dengan pergeseran kurva Lorenz, yang akan memengaruhi luas area di antara kurva dan garis diagonal, sehingga mengubah nilai Koefisien Gini.
Interpretasi Kurva Lorenz
Membaca dan menginterpretasi Kurva Lorenz melibatkan pengamatan jarak antara kurva dan garis diagonal. Semakin jauh kurva dari garis diagonal, semakin besar ketimpangan distribusi. Informasi yang diperoleh meliputi tingkat ketimpangan, perbandingan distribusi antar kelompok atau periode waktu, dan identifikasi kelompok populasi yang memiliki proporsi sumber daya yang lebih besar.
Contoh kasus studi: Analisis distribusi pendapatan di Indonesia pada tahun 2020 dan 2023 menggunakan Kurva Lorenz dapat menunjukkan apakah ketimpangan pendapatan meningkat atau menurun. Perbandingan kurva untuk dua tahun tersebut akan memberikan gambaran yang lebih jelas.
Keterbatasan Kurva Lorenz terletak pada ketidakmampuannya untuk mengidentifikasi penyebab ketimpangan. Ia hanya menunjukkan tingkat ketimpangan, bukan faktor-faktor yang mendasarinya. Selain itu, interpretasi kurva membutuhkan pemahaman yang mendalam tentang konteks data yang digunakan.
Ilustrasi Kurva Lorenz yang menunjukkan distribusi pendapatan merata akan menampilkan kurva yang hampir berhimpit dengan garis diagonal. Sebaliknya, ilustrasi distribusi tidak merata akan menunjukkan kurva yang jauh dari garis diagonal, dengan bagian bawah kurva yang lebih datar dan bagian atas yang lebih curam, menunjukkan konsentrasi kekayaan pada sebagian kecil populasi.
Penerapan Kurva Lorenz dalam Berbagai Bidang, Kurva Lorenz: Pengertian Dan Interpretasinya
Kurva Lorenz tidak hanya terbatas pada analisis ekonomi, tetapi juga dapat diterapkan di berbagai bidang lain. Kegunaannya terletak pada kemampuannya untuk memvisualisasikan dan mengukur ketimpangan distribusi berbagai sumber daya.
Contoh penerapan dalam bidang kesehatan adalah menganalisis distribusi akses layanan kesehatan. Kurva Lorenz dapat menunjukkan seberapa merata akses layanan kesehatan didistribusikan di antara populasi. Akses yang tidak merata dapat disebabkan oleh berbagai faktor seperti lokasi geografis, tingkat pendapatan, atau asuransi kesehatan.
Kurva Lorenz juga dapat digunakan untuk menganalisis distribusi tanah, pendidikan, dan sumber daya lainnya. Dalam bidang pendidikan, misalnya, kurva dapat menunjukkan distribusi akses terhadap pendidikan berkualitas di antara berbagai kelompok masyarakat.
Manfaat penggunaan Kurva Lorenz dalam pengambilan keputusan kebijakan publik adalah memberikan gambaran yang jelas tentang ketimpangan dan membantu dalam merumuskan kebijakan yang lebih efektif dan tepat sasaran untuk mengurangi ketimpangan tersebut.
Contoh kasus penerapan Kurva Lorenz dalam bidang pendidikan:
- Pengumpulan data: Mengumpulkan data jumlah siswa di setiap sekolah berdasarkan tingkat ekonomi keluarga.
- Pengolahan data: Mengurutkan data dari terendah ke tertinggi, menghitung persentase kumulatif siswa dan persentase kumulatif akses ke sekolah berkualitas.
- Pembuatan Kurva Lorenz: Membangun kurva Lorenz dengan menggunakan data yang telah diolah.
- Perhitungan Koefisien Gini: Menghitung Koefisien Gini untuk mengukur tingkat ketimpangan akses pendidikan.
- Interpretasi: Menganalisis hasil dan merumuskan kebijakan untuk mengurangi ketimpangan akses pendidikan.
Penutupan Akhir: Kurva Lorenz: Pengertian Dan Interpretasinya
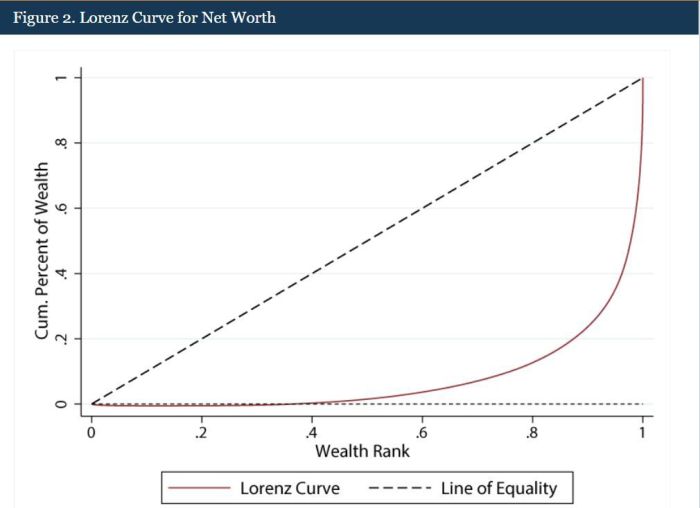
Kurva Lorenz, lebih dari sekadar grafik, ia adalah cerminan nyata dari keadilan sosial ekonomi. Dengan memahami cara kerjanya dan menginterpretasikannya dengan tepat, kita dapat melihat gambaran jelas tentang distribusi kekayaan dan pendapatan. Informasi ini tak hanya penting bagi para ekonom, tetapi juga untuk kita semua dalam memahami kondisi masyarakat dan mendorong terciptanya kebijakan yang lebih adil dan merata.
Jadi, mari kita gunakan kekuatan visualisasi data ini untuk membangun masa depan yang lebih baik!
Ringkasan FAQ
Apa perbedaan utama antara Kurva Lorenz dan Kurva Pareto?
Kurva Lorenz fokus pada distribusi kumulatif suatu variabel, sementara Kurva Pareto menggambarkan distribusi frekuensi variabel tersebut. Kurva Pareto sering digunakan untuk menganalisis fenomena “80/20 rule”.
Bagaimana Kurva Lorenz dapat diterapkan dalam bidang lingkungan?
Kurva Lorenz dapat digunakan untuk menganalisis distribusi polusi udara atau pencemaran air di berbagai wilayah, membantu mengidentifikasi daerah yang paling terdampak dan merumuskan strategi mitigasi yang tepat.
Apakah Kurva Lorenz memiliki keterbatasan?
Ya, Kurva Lorenz tidak memberikan informasi tentang mobilitas sosial atau dinamika perubahan distribusi dari waktu ke waktu.