Matriks Diagonal: Pengertian Dan Contohnya Dalam Matematika, siapa sangka konsep matematika ini ternyata begitu menarik dan punya peran penting? Bayangkan sebuah matriks, sebuah susunan angka yang rapi, tetapi hanya angka-angka pada diagonal utamanya yang bernilai, sisanya nol. Inilah pesona matriks diagonal, suatu struktur yang sederhana namun menyimpan kekuatan dalam berbagai aplikasi matematika.
Artikel ini akan mengupas tuntas pengertian matriks diagonal, menunjukkan contoh-contohnya, menjelaskan sifat-sifatnya, serta mengungkap bagaimana matriks ini digunakan dalam berbagai perhitungan dan aplikasi. Siap-siap terpesona dengan keindahan dan kegunaan matriks diagonal dalam dunia matematika!
Matriks Diagonal: Pengertian dan Contohnya: Matriks Diagonal: Pengertian Dan Contohnya Dalam Matematika
Hai, Bela! Pernah dengar istilah matriks diagonal? Kedengarannya agak rumit, ya? Padahal, kalau kita pahami dengan baik, matriks diagonal ini sebenarnya cukup menarik dan punya peran penting dalam berbagai bidang matematika. Artikel ini akan membahas pengertian, sifat-sifat, operasi, dan contoh penerapan matriks diagonal dengan cara yang mudah dipahami, jadi siap-siap ya untuk menjelajahi dunia matriks yang menyenangkan ini!
Pengertian Matriks Diagonal
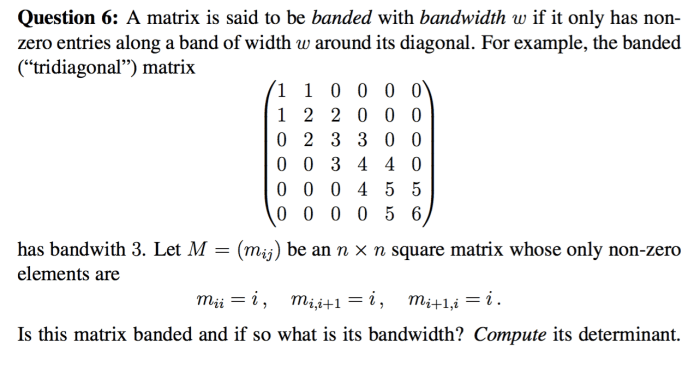
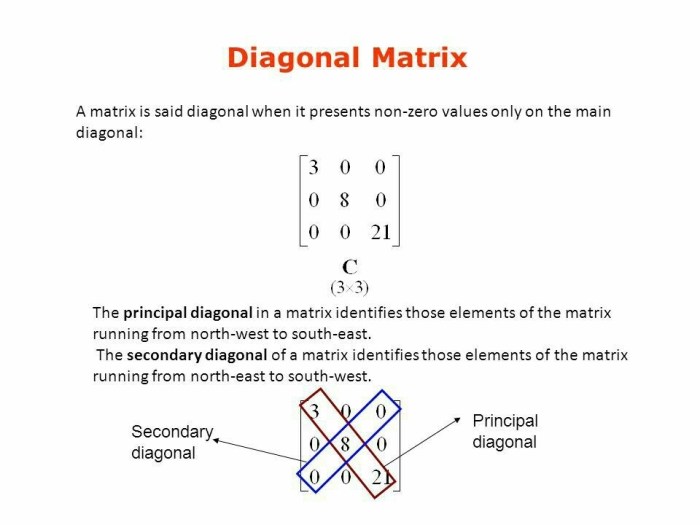
Matriks diagonal adalah matriks persegi (jumlah baris sama dengan jumlah kolom) di mana semua elemen di luar diagonal utama bernilai nol. Diagonal utama sendiri adalah garis diagonal yang membentang dari elemen pojok kiri atas ke pojok kanan bawah matriks. Elemen-elemen pada diagonal utama bisa bernilai nol atau bukan nol.
Contoh matriks diagonal:
Matriks diagonal 2×2:
[[2, 0],
[0, 5]]
Matriks diagonal 3×3:
[[1, 0, 0],
[0, -3, 0],
[0, 0, 4]]
Matriks diagonal 4×4:
[[0, 0, 0, 0],
[0, 7, 0, 0],
[0, 0, -2, 0],
[0, 0, 0, 9]]
Perbedaan matriks diagonal dengan matriks persegi dan matriks identitas:
Matriks persegi adalah matriks yang jumlah baris dan kolomnya sama. Matriks diagonal adalah kasus khusus dari matriks persegi. Sedangkan matriks identitas adalah matriks persegi di mana semua elemen pada diagonal utama bernilai 1 dan elemen lainnya bernilai 0.
| Jenis Matriks | Definisi | Contoh (3×3) | Ciri Khas |
|---|---|---|---|
| Matriks Diagonal | Matriks persegi dengan elemen di luar diagonal utama bernilai nol. | [[2, 0, 0], [0, -1, 0], [0, 0, 3]] |
Elemen non-nol hanya pada diagonal utama. |
| Matriks Persegi | Jumlah baris sama dengan jumlah kolom. | [[1, 2, 3], [4, 5, 6], [7, 8, 9]] |
Jumlah baris = jumlah kolom. |
| Matriks Identitas | Matriks persegi dengan elemen diagonal utama bernilai 1 dan elemen lainnya 0. | [[1, 0, 0], [0, 1, 0], [0, 0, 1]] |
Diagonal utama bernilai 1, lainnya 0. |
Ilustrasi matriks diagonal 3×3:
Misalnya, matriks [[a, 0, 0], [0, b, 0], [0, 0, c]]. ‘a’, ‘b’, dan ‘c’ mewakili elemen-elemen pada diagonal utama, sedangkan angka 0 mewakili elemen-elemen di luar diagonal utama yang semuanya bernilai nol.
Sifat-Sifat Matriks Diagonal

Matriks diagonal memiliki beberapa sifat unik yang memudahkan perhitungan. Berikut beberapa sifat pentingnya:
- Komutatif terhadap perkalian: Urutan perkalian dua matriks diagonal tidak mempengaruhi hasil.
- Invers matriks diagonal mudah dihitung: Invers didapatkan dengan membalik nilai setiap elemen pada diagonal utama.
- Determinan matriks diagonal adalah hasil kali elemen diagonal utamanya.
- Transpose matriks diagonal sama dengan dirinya sendiri.
- Perkalian matriks diagonal dengan matriks lain relatif sederhana.
Contoh perhitungan:
Sifat Komutatif:
Misal A = [[2, 0], [0, 3]] dan B = [[1, 0], [0, 4]].
Maka A x B = [[2, 0], [0, 12]] dan B x A = [[2, 0], [0, 12]]. Hasilnya sama.
Determinan:
Determinan matriks A = [[2, 0], [0, 3]] adalah 2 x 3 = 6.
Contoh perkalian dua matriks diagonal:
A = [[2, 0], [0, 3]] dan B = [[1, 0], [0, 4]]. Hasil perkalian A x B adalah [[2, 0], [0, 12]]. Perhatikan bahwa perkalian hanya dilakukan pada elemen-elemen diagonal utama.
Perbandingan dengan matriks simetris:
Matriks simetris adalah matriks yang sama dengan transposenya. Matriks diagonal merupakan kasus khusus dari matriks simetris, karena transposenya sama dengan dirinya sendiri.
Ringkasan sifat-sifat penting matriks diagonal:
- Komutatif pada perkalian
- Determinan mudah dihitung
- Transpose sama dengan dirinya sendiri
- Invers mudah dihitung
- Perkalian dengan matriks lain relatif sederhana
Operasi pada Matriks Diagonal, Matriks Diagonal: Pengertian Dan Contohnya Dalam Matematika
Operasi penjumlahan, pengurangan, dan perkalian pada matriks diagonal relatif mudah dilakukan.
Penjumlahan dan pengurangan:
Penjumlahan dan pengurangan dilakukan dengan menjumlahkan atau mengurangi elemen-elemen yang bersesuaian pada diagonal utama. Elemen di luar diagonal utama tetap nol.
Contoh: A = [[2, 0], [0, 3]], B = [[1, 0], [0, 4]].
A + B = [[3, 0], [0, 7]]
A – B = [[1, 0], [0, -1]]
Perkalian dengan skalar:
Perkalian matriks diagonal dengan skalar dilakukan dengan mengalikan setiap elemen pada diagonal utama dengan skalar tersebut.
Contoh: A = [[2, 0], [0, 3]], skalar k = 2.
k x A = [[4, 0], [0, 6]]
Perkalian dua matriks diagonal:
Perkalian dua matriks diagonal menghasilkan matriks diagonal baru dengan elemen diagonal utama yang merupakan hasil kali elemen-elemen diagonal utama matriks yang dikalikan.
Contoh: A = [[2, 0], [0, 3]], B = [[1, 0], [0, 4]].
A x B = [[2, 0], [0, 12]]
Contoh aplikasi nyata:
Operasi pada matriks diagonal sering digunakan dalam transformasi geometri, khususnya scaling (perubahan skala) dan rotasi pada bidang dua dimensi atau tiga dimensi.
Pada matriks diagonal berukuran sangat besar, operasi komputasi dapat menjadi intensif dan membutuhkan waktu proses yang lama. Optimasi algoritma dan penggunaan perangkat keras yang mumpuni menjadi penting untuk mengatasi kendala ini.
Contoh Penerapan Matriks Diagonal dalam Matematika
Matriks diagonal memiliki aplikasi yang luas dalam berbagai bidang matematika.
Contoh penerapan:
- Aljabar Linear: Matriks diagonal digunakan dalam diagonalisasi matriks, yang menyederhanakan perhitungan pangkat matriks dan solusi sistem persamaan linear.
- Kalkulus: Matriks diagonal muncul dalam konteks diferensial persamaan dan persamaan diferensial parsial.
- Statistika: Matriks kovarians dari variabel acak yang tidak berkorelasi adalah matriks diagonal.
Contoh penyelesaian sistem persamaan linear:
Sistem persamaan linear dengan matriks koefisien diagonal mudah diselesaikan karena setiap persamaan hanya melibatkan satu variabel.
Ilustrasi penerapan dalam transformasi geometri:
Matriks diagonal dapat merepresentasikan transformasi scaling (perubahan skala) pada suatu objek geometri. Misalnya, matriks [[2, 0], [0, 3]] akan menskalakan objek dua kali lipat pada sumbu x dan tiga kali lipat pada sumbu y.
Penggunaan matriks diagonal seringkali menyederhanakan perhitungan kompleks dalam aljabar linear dan bidang matematika lainnya, karena sifat-sifatnya yang unik dan operasi yang relatif mudah.
Ringkasan Terakhir
Memahami matriks diagonal bukan hanya sekadar mempelajari definisi dan rumus. Lebih dari itu, kita diajak untuk mengapresiasi keindahan dan efisiensi matematika dalam menyelesaikan permasalahan kompleks. Dari sifat-sifatnya yang unik hingga penerapannya yang luas, matriks diagonal membuktikan bahwa kesederhanaan dapat menyimpan kekuatan luar biasa. Semoga pemahaman kita tentang matriks diagonal semakin dalam dan menginspirasi kita untuk terus menjelajahi keajaiban matematika!
Pertanyaan Umum (FAQ)
Apa perbedaan utama antara matriks diagonal dan matriks segitiga?
Matriks diagonal hanya memiliki elemen non-nol pada diagonal utama, sedangkan matriks segitiga (atas atau bawah) memiliki elemen non-nol pada dan di atas/bawah diagonal utama.
Bisakah matriks diagonal berukuran 1×1?
Ya, matriks berukuran 1×1 dengan satu elemen tunggal juga merupakan matriks diagonal.
Apakah invers dari setiap matriks diagonal selalu ada?
Tidak, hanya matriks diagonal yang elemen diagonal utamanya tidak ada yang nol yang memiliki invers.
Apa aplikasi matriks diagonal dalam ilmu komputer?
Matriks diagonal digunakan dalam berbagai algoritma, termasuk dalam grafik komputer dan pemrosesan gambar.