Penjelasan Lengkap Tentang Translasi Dalam Matematika Dan Contoh Soal: Pernahkah kamu merasa pusing tujuh keliling saat berhadapan dengan soal matematika, khususnya yang berkaitan dengan geometri? Tenang, kali ini kita akan mengupas tuntas tentang translasi, sebuah konsep geometri yang mungkin terlihat rumit, tapi sebenarnya sangat menarik dan mudah dipahami jika dijelaskan dengan benar. Siap-siap untuk menjelajahi dunia translasi, dari definisi hingga penerapannya dalam kehidupan sehari-hari! Kita akan belajar rumus, notasi, dan berbagai contoh soal, mulai dari yang mudah hingga yang menantang.
Jadi, siapkan pena dan kertasmu, mari kita mulai petualangan matematika yang seru ini!
Translasi dalam matematika, khususnya geometri, adalah proses memindahkan suatu titik atau bangun geometri dari satu posisi ke posisi lain tanpa merubah bentuk dan ukurannya. Bayangkan seperti menggeser objek pada layar komputer; objek tersebut tetap sama, hanya posisinya yang berubah. Kita akan mempelajari bagaimana cara menghitung posisi baru suatu titik atau bangun setelah ditranslasikan, baik secara manual maupun dengan menggunakan rumus.
Dengan contoh-contoh soal yang beragam dan pembahasan yang detail, kamu akan memahami konsep translasi dengan mudah dan percaya diri dalam menghadapinya.
Translasi dalam Matematika: Panduan Lengkap untuk Pemula: Penjelasan Lengkap Tentang Translasi Dalam Matematika Dan Contoh Soal
Pernahkah kamu memperhatikan bagaimana sebuah gambar bisa dipindahkan ke tempat lain tanpa mengubah bentuknya? Itulah konsep dasar dari translasi dalam matematika, sebuah transformasi geometri yang sangat penting dan memiliki aplikasi luas, mulai dari desain grafis hingga rekayasa sipil. Yuk, kita telusuri lebih dalam tentang dunia translasi!
Definisi Translasi dalam Geometri
Translasi dalam geometri adalah transformasi yang memindahkan setiap titik pada suatu objek sejauh jarak tertentu dan ke arah tertentu tanpa mengubah ukuran atau bentuk objek tersebut. Bayangkan kamu menggeser sebuah kartu pos di atas meja; kartu pos tersebut mengalami translasi. Posisi titik-titik penyusun kartu pos berubah, tetapi bentuk dan ukurannya tetap sama.
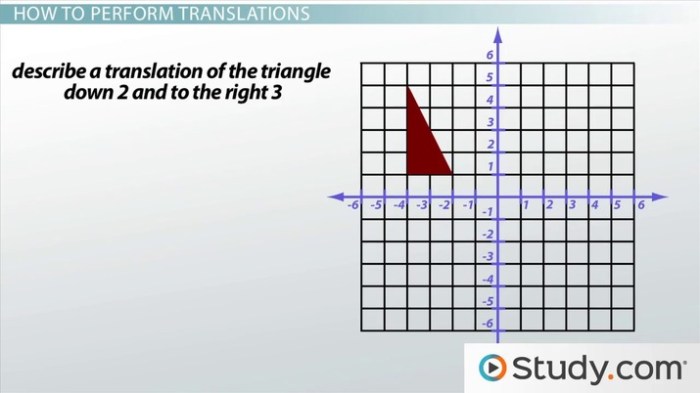
Contoh Translasi pada Bidang Kartesius
Pada bidang kartesius, translasi digambarkan sebagai pergeseran titik-titik koordinat. Misalnya, jika titik (2,3) digeser 3 satuan ke kanan dan 2 satuan ke atas, maka titik tersebut akan berpindah ke posisi (5,5). Pergeseran ini disebut vektor translasi.
Ilustrasi Translasi Titik (x,y)
Mari kita bayangkan titik (x,y) pada bidang kartesius. Jika titik ini ditranslasikan sejauh ‘a’ satuan ke kanan dan ‘b’ satuan ke atas, maka koordinat titik baru akan menjadi (x+a, y+b). Prosesnya sederhana: tambahkan nilai ‘a’ pada koordinat x dan nilai ‘b’ pada koordinat y. Arah pergeseran ke kanan dilambangkan dengan nilai ‘a’ positif, dan ke kiri dengan nilai ‘a’ negatif.
Begitu pula, arah pergeseran ke atas dilambangkan dengan nilai ‘b’ positif, dan ke bawah dengan nilai ‘b’ negatif.
Tabel Koordinat Titik Sebelum dan Sesudah Translasi
| Titik Awal (x,y) | Pergeseran (a,b) | Titik Akhir (x+a, y+b) |
|---|---|---|
| (2,3) | (3,-2) | (5,1) |
Perbedaan Translasi dan Rotasi
Translasi dan rotasi sama-sama transformasi geometri, tetapi mekanismenya berbeda. Translasi hanya menggeser objek tanpa mengubah orientasinya, sementara rotasi memutar objek di sekitar suatu titik pusat, sehingga orientasinya berubah. Bayangkan kamu menggeser foto di meja (translasi) versus memutar foto tersebut (rotasi).
Rumus dan Notasi Translasi
Rumus umum translasi untuk titik (x,y) dengan vektor translasi (a,b) adalah (x’, y’) = (x+a, y+b), di mana (x’, y’) adalah koordinat titik setelah translasi. Notasi yang umum digunakan adalah T(a,b) untuk mewakili translasi dengan vektor (a,b).
Contoh Penerapan Rumus Translasi
Misalnya, titik A(1,2) ditranslasikan dengan vektor T(3,-1). Maka koordinat bayangan A’ adalah (1+3, 2+(-1)) = (4,1).
Contoh Soal dan Penyelesaiannya
Tentukan bayangan titik B(-2,5) setelah ditranslasikan oleh vektor T(-1,2).
- Identifikasi titik awal: B(-2,5)
- Identifikasi vektor translasi: T(-1,2)
- Terapkan rumus translasi: (x’, y’) = (x+a, y+b)
- Substitusikan nilai: (x’, y’) = (-2 + (-1), 5 + 2)
- Hitung koordinat bayangan: (x’, y’) = (-3,7)
Translasi pada Berbagai Bentuk Geometri
Konsep translasi dapat diterapkan pada berbagai bentuk geometri. Berikut beberapa contohnya:
Translasi pada Segitiga
Jika sebuah segitiga ditranslasikan, setiap titik sudutnya akan berpindah sejauh dan searah yang sama. Misalnya, segitiga dengan titik sudut A(1,1), B(3,1), dan C(2,3) ditranslasikan dengan vektor T(2,1), maka titik sudut bayangannya akan menjadi A'(3,2), B'(5,2), dan C'(4,4). Bentuk segitiga tetap sama, hanya posisinya yang berubah.
Translasi pada Persegi Panjang
Sama seperti segitiga, translasi pada persegi panjang juga memindahkan semua titik sudutnya sejauh dan searah yang sama. Jika setiap titik sudut persegi panjang ditranslasikan dengan vektor yang sama, bentuk dan ukuran persegi panjang tetap terjaga.
Contoh Soal Translasi pada Trapesium, Penjelasan Lengkap Tentang Translasi Dalam Matematika Dan Contoh Soal
Sebuah trapesium ABCD dengan koordinat A(1,1), B(4,1), C(5,3), dan D(2,3) ditranslasikan dengan vektor T(-2,3). Tentukan koordinat bayangan trapesium tersebut.
- Tentukan koordinat setiap titik sudut trapesium.
- Terapkan rumus translasi pada setiap titik sudut: (x’, y’) = (x – 2, y + 3).
- Hitung koordinat bayangan setiap titik sudut.
- Gambar trapesium awal dan bayangannya untuk memverifikasi hasil.
Perlu diingat bahwa efek translasi pada bangun datar berbeda bergantung pada bentuk dan ukuran bangun datar tersebut. Namun, prinsip dasarnya tetap sama: semua titik berpindah sejauh dan searah yang sama.
Penerapan Translasi dalam Kehidupan Sehari-hari
Translasi bukan hanya konsep abstrak dalam matematika, tetapi juga memiliki banyak aplikasi praktis dalam kehidupan sehari-hari.
Contoh Penerapan Translasi
- Animasi Komputer: Gerakan karakter dalam animasi komputer seringkali menggunakan prinsip translasi untuk memindahkan karakter dari satu titik ke titik lainnya.
- Desain Grafis: Menggeser objek dalam perangkat lunak desain grafis adalah contoh penerapan translasi.
- Rekayasa Sipil: Perencanaan tata letak bangunan dan infrastruktur seringkali melibatkan translasi untuk memindahkan objek virtual di dalam model digital.
Ilustrasi Penerapan Translasi dalam Bidang Teknik
Dalam desain CAD (Computer-Aided Design), arsitek atau insinyur sering memindahkan komponen bangunan (misalnya, jendela, pintu) dengan menggunakan translasi. Mereka hanya perlu menentukan vektor translasi untuk memindahkan komponen tersebut ke posisi yang diinginkan tanpa mengubah ukuran atau orientasinya.
Tabel Penerapan Translasi dalam Berbagai Bidang
| Bidang | Penerapan | Contoh |
|---|---|---|
| Animasi | Memindahkan karakter | Gerakan karakter dalam film animasi |
| Desain Grafis | Menggeser objek | Memindahkan gambar pada layout desain |
| Rekayasa | Perencanaan tata letak | Memindahkan komponen bangunan dalam desain CAD |
Contoh Soal dan Pembahasan Translasi
Berikut beberapa contoh soal translasi dengan tingkat kesulitan yang berbeda:
Contoh Soal 1 (Mudah)
Tentukan bayangan titik P(2, -1) jika ditranslasikan oleh vektor T(3, 2).
Pembahasan: (2+3, -1+2) = (5, 1)
Contoh Soal 2 (Sedang)
Sebuah segitiga ABC dengan koordinat A(1,2), B(3,4), dan C(5,2) ditranslasikan oleh vektor T(-1,3). Tentukan koordinat bayangan segitiga tersebut.
Pembahasan: A'(0,5), B'(2,7), C'(4,5)
Contoh Soal 3 (Sulit)
Sebuah persegi panjang ABCD dengan koordinat A(-2,1), B(2,1), C(2,-1), dan D(-2,-1) ditranslasikan oleh T(x,y) sehingga bayangannya adalah A'(0,3), B'(4,3), C'(4,1), dan D'(0,1). Tentukan nilai x dan y.
Pembahasan: Dengan membandingkan koordinat A dan A’, kita dapatkan x = 2 dan y = 2.
Tips untuk menyelesaikan soal translasi: Identifikasi titik awal, vektor translasi, dan rumus translasi. Lakukan perhitungan dengan teliti dan verifikasi hasil dengan menggambar jika diperlukan.
Contoh Soal Cerita
Sebuah mobil bergerak ke timur sejauh 5 km dan ke utara sejauh 3 km. Gambarkan pergerakan mobil tersebut sebagai translasi pada bidang kartesius dan tentukan koordinat posisi akhir mobil jika posisi awalnya adalah (0,0).
Pembahasan: Pergerakan mobil tersebut dapat direpresentasikan sebagai translasi dengan vektor T(5,3). Koordinat posisi akhir mobil adalah (5,3).
Kesimpulan
Memahami translasi dalam matematika ternyata tidak sesulit yang dibayangkan, bukan? Setelah mempelajari definisi, rumus, penerapan pada berbagai bangun geometri, dan contoh soal yang beragam, sekarang kamu memiliki pemahaman yang komprehensif tentang konsep ini. Lebih dari sekedar teori, translasi ternyata memiliki aplikasi yang luas dalam kehidupan nyata, mulai dari bidang teknik hingga desain grafis. Jadi, jangan ragu untuk terus mengasah kemampuanmu dalam matematika, karena setiap konsep yang kamu kuasai akan membuka pintu menuju pemahaman yang lebih luas dan mendalam.
Selamat berpetualang dalam dunia matematika yang menakjubkan!
Daftar Pertanyaan Populer
Apa perbedaan antara translasi dan refleksi?
Translasi menggeser objek, sedangkan refleksi memantulkan objek terhadap suatu garis.
Bisakah translasi diterapkan pada bangun ruang?
Ya, konsep translasi juga berlaku pada bangun ruang, hanya saja perhitungannya akan melibatkan tiga dimensi (x, y, z).
Bagaimana cara menentukan arah translasi jika hanya diberikan titik awal dan titik akhir?
Kurangi koordinat titik awal dari koordinat titik akhir. Hasilnya menunjukkan vektor translasi (a, b).